Difference between revisions of "Mean Average"
(→Calculating a Mean Average) |
|||
| Line 44: | Line 44: | ||
===Calculating a Mean Average=== | ===Calculating a Mean Average=== | ||
Results: 5,3 | Results: 5,3 | ||
| − | + | ||
| − | + | <math>Average = \tfrac{5+3}{2}</math> | |
| + | |||
| + | <math>Average = 4</math> | ||
Results: 7.0, 6.8, 7.8 | Results: 7.0, 6.8, 7.8 | ||
| − | + | ||
| − | + | <math>Average = \tfrac{7.0+6.8+7.8}{3}</math> | |
| + | |||
| + | <math>Average = 7.1</math> | ||
Results: 12.3, 11.7, 11.4, 12.1 | Results: 12.3, 11.7, 11.4, 12.1 | ||
| − | + | ||
| − | + | <math>Average = \tfrac{12.3+11.7+11.4+12.1}{4}</math> | |
| + | |||
| + | <math>Average = 11.875</math> | ||
In science the answer should be rounded to the same number of [[Significant Figures|significant figures]] as the original numbers. | In science the answer should be rounded to the same number of [[Significant Figures|significant figures]] as the original numbers. | ||
| − | + | ||
| + | <math>Average = 11.9</math> | ||
===Examples=== | ===Examples=== | ||
Revision as of 13:24, 7 June 2019
Contents
Key Stage 3
Meaning
A mean average is when you add up a set of numbers and divide by how many of numbers were added.
About a Mean Average
- A mean average is used in science to reduce the effects of random errors in the results of an experiment.
Calculating a Mean Average
Results: 5,3
\(Average = \tfrac{5+3}{2}\)
\(Average = 4\)
Results: 7.0, 6.8, 7.8
\(Average = \tfrac{7.0+6.8+7.8}{3}\)
\(Average = 7.1\)
Results: 12.3, 11.7, 11.4, 12.1
\(Average = \tfrac{12.3+11.7+11.4+12.1}{4}\)
\(Average = 11.875\) In science the answer should be rounded to the same number of significant figures as the original numbers.
\(Average = 11.9\)
Examples
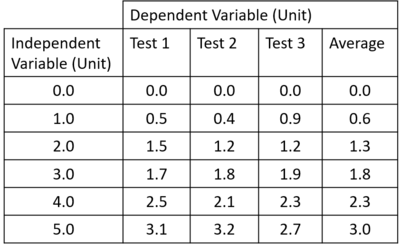
| The average for each set of results can be calculated by adding a row together and dividing by the number of results in that row. |
Key Stage 4
Meaning
A mean average is when you add up a set of numbers and divide by how many of numbers were added.
About a Mean Average
- A mean average is used in science to reduce the effects of random errors in the results of an experiment.
Calculating a Mean Average
Results: 5,3
\(Average = \tfrac{5+3}{2}\)
\(Average = 4\)
Results: 7.0, 6.8, 7.8
\(Average = \tfrac{7.0+6.8+7.8}{3}\)
\(Average = 7.1\)
Results: 12.3, 11.7, 11.4, 12.1
\(Average = \tfrac{12.3+11.7+11.4+12.1}{4}\)
\(Average = 11.875\) In science the answer should be rounded to the same number of significant figures as the original numbers.
\(Average = 11.9\)
Examples
| The average for each set of results can be calculated by adding a row together and dividing by the number of results in that row. |