Difference between revisions of "Velocity-Time Graph"
(→Calculating Distance Travelled) |
(→Example Calculations) |
||
| Line 67: | Line 67: | ||
|} | |} | ||
| + | {| class="wikitable" | ||
| + | | style="height:20px; width:500px; text-align:left;" colspan = "3"|'''Calculate the [[acceleration]] of the [[object]] at each stage in this journey.''' | ||
| + | |- | ||
| + | |colspan = "3"[[File:vtGraph1.png|center|500px]] | ||
| + | |- | ||
| + | | style="height:20px; width:300px; text-align:left;" |'''State the known [[variable]]s.''' | ||
| + | [[File:vtGraphCalculateAcceleration3.png|centre|300px]] | ||
| + | v = 40m/s | ||
| + | |||
| + | u = 20m/s | ||
| + | |||
| + | t = 8s | ||
| + | |- | ||
| + | | style="height:20px; width:200px; text-align:left;" |'''2. [[Substitute (Maths)|Substitute]] the numbers into the [[equation]] and [[Solve (Maths)|solve]].''' | ||
| + | |||
| + | <math>a = \frac{v-u}{t}</math> | ||
| + | |||
| + | <math>a = \frac{40-20}{8}</math> | ||
| + | |||
| + | <math>a = \frac{20}{8}</math> | ||
| + | |||
| + | <math>a = 2.5m/s/s</math> | ||
| + | | style="height:20px; width:200px; text-align:left;" |'''2. [[Substitute (Maths)|Substitute]] the numbers into the [[equation]] and [[Solve (Maths)|solve]].''' | ||
| + | |||
| + | <math>a = \frac{v-u}{t}</math> | ||
| + | |||
| + | <math>a = \frac{10-40}{8}</math> | ||
| + | |||
| + | <math>a = \frac{-30}{8}</math> | ||
| + | |||
| + | <math>a = -3.75m/s/s</math> | ||
| + | |} | ||
====Calculating Distance Travelled==== | ====Calculating Distance Travelled==== | ||
: The [[distance]] travelled can be calculated from a '''velocity-time graph''' by breaking the [[graph]] into simple shapes and finding the [[area]] of those shapes. This may use the equations <math>area = base \times height</math> for rectangular shapes and <math>area = \frac{base \times height}{2}</math> for triangular shapes. | : The [[distance]] travelled can be calculated from a '''velocity-time graph''' by breaking the [[graph]] into simple shapes and finding the [[area]] of those shapes. This may use the equations <math>area = base \times height</math> for rectangular shapes and <math>area = \frac{base \times height}{2}</math> for triangular shapes. | ||
Revision as of 13:02, 14 February 2019
Contents
Key Stage 4
Meaning
A velocity-time graph is a graph that shows how the velocity of an object changes with time.
About Velocity Time Graphs
- Velocity-time graphs give information about the journey taken by an object.
- On a velocity-time graph the velocity is plotted on the y-axis and the time is plotted on the x-axis.
- A velocity-time graph can be used to calculate the acceleration of an object or the distance travelled by the object.
- The gradient of a velocity-time graph is the same as the acceleration.
- The area under the curve on a velocity-time graph is the distance travelled by an object.
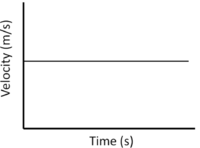
| Constant Velocity | Accelerating | Decelerating |
| A gradient of zero shows the object is travelling at a constant velocity. | Acceleration is shown by a positive gradient. | Deceleration is shown by a negative gradient. |
Example Calculations
Calculating Acceleration
- The acceleration can be calculated from a velocity-time graph by reading the graph and using the equation \(a=\frac{v-u}{t}\).
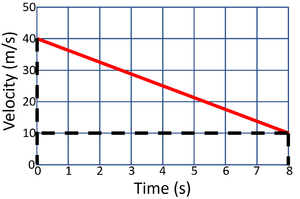
| Calculate the acceleration of the object in this journey. | Calculate the acceleration of the object in this journey. |
| State the known variables.
v = 40m/s u = 20m/s t = 8s |
State the known variables.
v = 10m/s u = 40m/s t = 8s |
| 2. Substitute the numbers into the equation and solve.
\(a = \frac{v-u}{t}\) \(a = \frac{40-20}{8}\) \(a = \frac{20}{8}\) \(a = 2.5m/s/s\) |
2. Substitute the numbers into the equation and solve.
\(a = \frac{v-u}{t}\) \(a = \frac{10-40}{8}\) \(a = \frac{-30}{8}\) \(a = -3.75m/s/s\) |
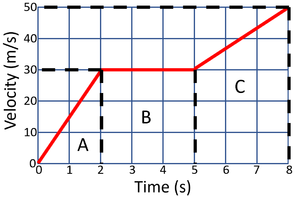
| Calculate the acceleration of the object at each stage in this journey. | ||
| colspan = "3" | ||
| State the known variables.
v = 40m/s u = 20m/s t = 8s | ||
| 2. Substitute the numbers into the equation and solve.
\(a = \frac{v-u}{t}\) \(a = \frac{40-20}{8}\) \(a = \frac{20}{8}\) \(a = 2.5m/s/s\) |
2. Substitute the numbers into the equation and solve.
\(a = \frac{v-u}{t}\) \(a = \frac{10-40}{8}\) \(a = \frac{-30}{8}\) \(a = -3.75m/s/s\) | |
Calculating Distance Travelled
- The distance travelled can be calculated from a velocity-time graph by breaking the graph into simple shapes and finding the area of those shapes. This may use the equations \(area = base \times height\) for rectangular shapes and \(area = \frac{base \times height}{2}\) for triangular shapes.
| Calculate the distance travelled by the object in this journey. | Calculate the distance travelled by the object in this journey. |
| 1. State the known quantities
base = 8s height = 30m/s |
1. State the known quantities
base = 8s height = 40m/s |
| 2. Substitute the numbers into the equation and solve.
\(area = b \times h\) \(area = 8 \times 30\) \(area = distance = 250m\) |
2. Substitute the numbers into the equation and solve.
\(area = \frac{b \times h}{2}\) \(area = \frac{8 \times 40}{2}\) \(area = \frac{320}{2}\) \(area = distance = 160m\) |