Open main menu
Key Stage Wiki β

Difference between revisions of "Distance-Time Graph"

(→‎Example Calculations)
 
(3 intermediate revisions by 2 users not shown)
Line 43: Line 43:
 
|-
 
|-
 
| style="height:20px; width:300px; text-align:left;" |'''Calculate the speed of the object in this 80 second journey.'''
 
| style="height:20px; width:300px; text-align:left;" |'''Calculate the speed of the object in this 80 second journey.'''
−
: distance = 400[[m]]
+
: distance = 400m
−
: time = 80[[s]]
+
: time = 80s
 
:<math>Speed = {\frac{distance}{time}} </math>
 
:<math>Speed = {\frac{distance}{time}} </math>
 
:<math>Speed = {\frac{400}{80}} </math>
 
:<math>Speed = {\frac{400}{80}} </math>
 
:<math>Speed = 5m/s </math>
 
:<math>Speed = 5m/s </math>
 
| style="height:20px; width:300px; text-align:left;" |'''Calculate the speed of the object in the first 20 seconds.'''
 
| style="height:20px; width:300px; text-align:left;" |'''Calculate the speed of the object in the first 20 seconds.'''
−
: distance = 400[[m]]
+
: distance = 400m
−
: time = 20[[s]]
+
: time = 20s
 
:<math>Speed = {\frac{distance}{time}} </math>
 
:<math>Speed = {\frac{distance}{time}} </math>
 
:<math>Speed = {\frac{400}{20}} </math>
 
:<math>Speed = {\frac{400}{20}} </math>
Line 59: Line 59:
 
|-
 
|-
 
| style="height:20px; width:300px; text-align:left;" |'''Calculate the speed of the object between 20 and 80 seconds.'''
 
| style="height:20px; width:300px; text-align:left;" |'''Calculate the speed of the object between 20 and 80 seconds.'''
−
: distance = 100[[m]]
+
: distance = 100m
−
: time = 60[[s]]
+
: time = 60s
 
:<math>Speed = {\frac{distance}{time}} </math>
 
:<math>Speed = {\frac{distance}{time}} </math>
 
:<math>Speed = {\frac{100}{60}} </math>
 
:<math>Speed = {\frac{100}{60}} </math>
 
:<math>Speed \approx 1.7m/s </math>
 
:<math>Speed \approx 1.7m/s </math>
 
| style="height:20px; width:300px; text-align:left;" |'''Calculate the average speed of the object for its journey.'''
 
| style="height:20px; width:300px; text-align:left;" |'''Calculate the average speed of the object for its journey.'''
−
: distance = 500[[m]]
+
: distance = 500m
−
: time = 80[[s]]
+
: time = 80s
 
:<math>Speed = {\frac{distance}{time}} </math>
 
:<math>Speed = {\frac{distance}{time}} </math>
 
:<math>Speed = {\frac{500}{80}} </math>
 
:<math>Speed = {\frac{500}{80}} </math>
Line 116: Line 116:
 
|-
 
|-
 
| style="height:20px; width:300px; text-align:left;" |'''Calculate the [[speed]] of the object in the first 10 seconds of the journey.'''
 
| style="height:20px; width:300px; text-align:left;" |'''Calculate the [[speed]] of the object in the first 10 seconds of the journey.'''
−
: distance = 200[[m]]
+
: distance = 200m
−
: time = 10[[s]]
+
: time = 10s
 
:<math>v= {\frac{distance}{time}} </math>
 
:<math>v= {\frac{distance}{time}} </math>
 
:<math>Speed = {\frac{200}{10}} </math>
 
:<math>Speed = {\frac{200}{10}} </math>
 
:<math>Speed = 20m/s </math>
 
:<math>Speed = 20m/s </math>
 
| style="height:20px; width:300px; text-align:left;" |'''Calculate the [[speed]] of the object in the first 10 seconds of the journey.'''
 
| style="height:20px; width:300px; text-align:left;" |'''Calculate the [[speed]] of the object in the first 10 seconds of the journey.'''
−
: distance = 70[[m]]
+
: distance = 70m
−
: time = 10[[s]]
+
: time = 10s
 
:<math>Speed = {\frac{distance}{time}} </math>
 
:<math>Speed = {\frac{distance}{time}} </math>
 
:<math>Speed = {\frac{70}{10}} </math>
 
:<math>Speed = {\frac{70}{10}} </math>
Line 135: Line 135:
 
|-
 
|-
 
| style="height:20px; width:300px; text-align:left;" |'''Calculate the average [[speed]] of the [[object]] over the entire journey.'''
 
| style="height:20px; width:300px; text-align:left;" |'''Calculate the average [[speed]] of the [[object]] over the entire journey.'''
−
: distance = 400[[m]]
+
: distance = 400m
−
: time = 80[[s]]
+
: time = 80s
−
:<math>v= {\frac{distance}{time}} </math>
+
:<math>Speed= {\frac{distance}{time}} </math>
 
:<math>Speed = {\frac{400}{80}} </math>
 
:<math>Speed = {\frac{400}{80}} </math>
 
:<math>Speed = 5m/s </math>
 
:<math>Speed = 5m/s </math>
 
| style="height:20px; width:300px; text-align:left;" |'''Calculate the average [[speed]] of the [[object]] over the entire journey.'''
 
| style="height:20px; width:300px; text-align:left;" |'''Calculate the average [[speed]] of the [[object]] over the entire journey.'''
−
: distance = 500[[m]]
+
: distance = 500m
−
: time = 80[[s]]
+
: time = 80s
 
:<math>Speed = {\frac{distance}{time}} </math>
 
:<math>Speed = {\frac{distance}{time}} </math>
 
:<math>Speed = {\frac{500}{80}} </math>
 
:<math>Speed = {\frac{500}{80}} </math>
 
:<math>Speed = 6.25m/s </math>
 
:<math>Speed = 6.25m/s </math>
 
|}
 
|}
 +
 +
 +
===References===
 +
====AQA====
 +
 +
:[https://www.amazon.co.uk/gp/product/0008158770/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=0008158770&linkCode=as2&tag=nrjc-21&linkId=ec31595e720e1529e49876c3866fff6e ''Distance-time graph, pages 140, 144-5, GCSE Physics; Student Book, Collins, AQA '']
 +
:[https://www.amazon.co.uk/gp/product/1782945598/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=1782945598&linkCode=as2&tag=nrjc-21&linkId=ad276ad49df77ab4b40ab4fd0fe09855 ''Distance-time graphs, page 210, GCSE Combined Science; The Revision Guide, CGP, AQA '']
 +
:[https://www.amazon.co.uk/gp/product/178294558X/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=178294558X&linkCode=as2&tag=nrjc-21&linkId=f0dfb66dafcb0c6e9449e7b1a4ae1ac94 ''Distance-time graphs, page 62, GCSE Physics; The Revision Guide, CGP, AQA '']
 +
:[https://www.amazon.co.uk/gp/product/019835939X/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=019835939X&linkCode=as2&tag=nrjc-21&linkId=57e96876985fc39b1a3d8a3e3dc238b6 ''Distance-time graphs, pages 134-135, 140, GCSE Physics; Third Edition, Oxford University Press, AQA '']
 +
:[https://www.amazon.co.uk/gp/product/1471851370/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=1471851370&linkCode=as2&tag=nrjc-21&linkId=01c69b0ae058f809cf636033e6ba793e ''Distance-time graphs, pages 149-50, GCSE Physics, Hodder, AQA '']
 +
:[https://www.amazon.co.uk/gp/product/1782946403/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=1782946403&linkCode=as2&tag=nrjc-21&linkId=32a0abb60dff015b15b50e9b1d7b4644 ''Distance-time graphs, pages 152, 153, GCSE Combined Science Trilogy; Physics, CGP, AQA '']
 +
:[https://www.amazon.co.uk/gp/product/1782945970/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=1782945970&linkCode=as2&tag=nrjc-21&linkId=a120d24dcc7cc7a58192069a3aafc1d2 ''Distance-time graphs, pages 183, 184, GCSE Physics; The Complete 9-1 Course for AQA, CGP, AQA '']
 +
:[https://www.amazon.co.uk/gp/product/1471851362/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=1471851362&linkCode=as2&tag=nrjc-21&linkId=7d78d70a2044ee9982dae010c94af92a ''Distance-time graphs, pages 227-8, GCSE Combined Science Trilogy 2, Hodder, AQA  '']
 +
 +
====OCR====
 +
:[https://www.amazon.co.uk/gp/product/1782945695/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=1782945695&linkCode=as2&tag=nrjc-21&linkId=ceafcc80bcad6b6754ee97a0c7ceea53 ''Distance-time graphs, page 161, Gateway GCSE Combined Science; The Revision Guide, CGP, OCR  '']
 +
:[https://www.amazon.co.uk/gp/product/1782945687/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=1782945687&linkCode=as2&tag=nrjc-21&linkId=9a598e52189317a20311d7a632747bc9 ''Distance-time graphs, page 24, Gateway GCSE Physics; The Revision Guide, CGP, OCR  '']

Latest revision as of 00:40, 5 December 2019

Key Stage 3

Meaning

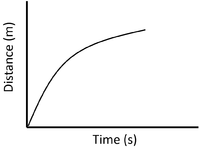
A distance time graph is a graph that shows how the distance of an object from the origin changes with time.

About Distance Time Graphs

Distance-time graphs give information about the journey taken by an object.
On a distance time graph the distance is plotted on the y-axis and the time is plotted on the x-axis.
A distance time graph can be used to calculate the speed of an object.
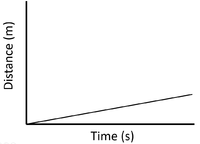
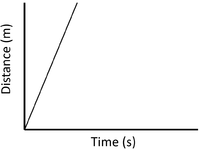
Slow Speed Medium Speed High Speed
DtGraphSlowSpeed.png
DtGraphMediumSpeed.png
DtGraphHighSpeed.png
A constant speed is shown by a constant positive gradient. A higher gradient means a higher speed. The highest speed is shown by the steepest gradient.
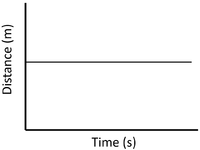
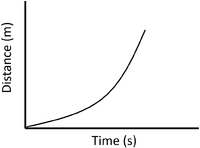
Stationary Accelerating Decelerating
DtGraphStationary.png
DtGraphAccelerating.png
DtGraphDecelerating.png
A gradient of zero shows the object is not moving. Acceleration is shown by an increasing gradient. Deceleration is shown by a decreasing gradient.


Example Calculations

The speed can be calculated from a distance time graph by reading the graph and using the equation Speed=Distance/Time.
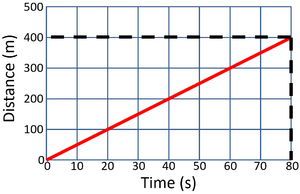
DtGraphCalculation1.png
DtGraphCalculation2.png
Calculate the speed of the object in this 80 second journey.
distance = 400m
time = 80s

\[Speed = {\frac{distance}{time}} \] \[Speed = {\frac{400}{80}} \] \[Speed = 5m/s \]

Calculate the speed of the object in the first 20 seconds.
distance = 400m
time = 20s

\[Speed = {\frac{distance}{time}} \] \[Speed = {\frac{400}{20}} \] \[Speed = 20m/s \]

DtGraphCalculation2.png
DtGraphCalculation2.png
Calculate the speed of the object between 20 and 80 seconds.
distance = 100m
time = 60s

\[Speed = {\frac{distance}{time}} \] \[Speed = {\frac{100}{60}} \] \[Speed \approx 1.7m/s \]

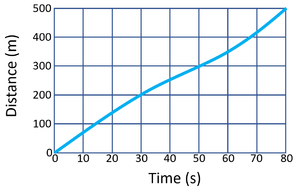
Calculate the average speed of the object for its journey.
distance = 500m
time = 80s

\[Speed = {\frac{distance}{time}} \] \[Speed = {\frac{500}{80}} \] \[Speed = 6.25m/s \]

Key Stage 4

Meaning

A distance time graph is a graph that shows how the distance of an object from the origin changes with time.

About Distance Time Graphs

Distance-time graphs give information about the journey taken by an object.
On a distance time graph the distance is plotted on the y-axis and the time is plotted on the x-axis.
A distance time graph can be used to calculate the speed of an object.
Slow Speed Medium Speed High Speed
DtGraphSlowSpeed.png
DtGraphMediumSpeed.png
DtGraphHighSpeed.png
A constant speed is shown by a constant positive gradient. A higher gradient means a higher speed. The highest speed is shown by the steepest gradient.
Stationary Accelerating Decelerating
DtGraphStationary.png
DtGraphAccelerating.png
DtGraphDecelerating.png
A gradient of zero shows the object is not moving. Acceleration is shown by an increasing gradient. Deceleration is shown by a decreasing gradient.


Example Calculations

The speed can be calculated from a distance time graph by reading the graph and using the equation Speed=Distance/Time.
DtGraphCalculation4.png
DtGraphCalculation5.png
Calculate the speed of the object in the first 10 seconds of the journey.
distance = 200m
time = 10s

\[v= {\frac{distance}{time}} \] \[Speed = {\frac{200}{10}} \] \[Speed = 20m/s \]

Calculate the speed of the object in the first 10 seconds of the journey.
distance = 70m
time = 10s

\[Speed = {\frac{distance}{time}} \] \[Speed = {\frac{70}{10}} \] \[Speed = 7m/s \]

DtGraphCalculation4.png
DtGraphCalculation5.png
Calculate the average speed of the object over the entire journey.
distance = 400m
time = 80s

\[Speed= {\frac{distance}{time}} \] \[Speed = {\frac{400}{80}} \] \[Speed = 5m/s \]

Calculate the average speed of the object over the entire journey.
distance = 500m
time = 80s

\[Speed = {\frac{distance}{time}} \] \[Speed = {\frac{500}{80}} \] \[Speed = 6.25m/s \]


References

AQA

Distance-time graph, pages 140, 144-5, GCSE Physics; Student Book, Collins, AQA
Distance-time graphs, page 210, GCSE Combined Science; The Revision Guide, CGP, AQA
Distance-time graphs, page 62, GCSE Physics; The Revision Guide, CGP, AQA
Distance-time graphs, pages 134-135, 140, GCSE Physics; Third Edition, Oxford University Press, AQA
Distance-time graphs, pages 149-50, GCSE Physics, Hodder, AQA
Distance-time graphs, pages 152, 153, GCSE Combined Science Trilogy; Physics, CGP, AQA
Distance-time graphs, pages 183, 184, GCSE Physics; The Complete 9-1 Course for AQA, CGP, AQA
Distance-time graphs, pages 227-8, GCSE Combined Science Trilogy 2, Hodder, AQA

OCR

Distance-time graphs, page 161, Gateway GCSE Combined Science; The Revision Guide, CGP, OCR
Distance-time graphs, page 24, Gateway GCSE Physics; The Revision Guide, CGP, OCR
Retrieved from "https://keystagewiki.com/index.php?title=Distance-Time_Graph&oldid=21007"