Difference between revisions of "Area"
| (12 intermediate revisions by the same user not shown) | |||
| Line 13: | Line 13: | ||
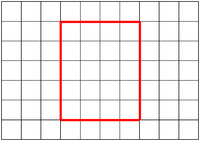
| style="height:20px; width:200px; text-align:center;" |The shape has 20 [[square]]s inside it, so the [[area]] is 20 [[square]]s. | | style="height:20px; width:200px; text-align:center;" |The shape has 20 [[square]]s inside it, so the [[area]] is 20 [[square]]s. | ||
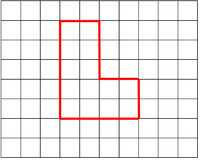
| style="height:20px; width:200px; text-align:center;" |This shape has an [[area]] of 14 [[square]]s. | | style="height:20px; width:200px; text-align:center;" |This shape has an [[area]] of 14 [[square]]s. | ||
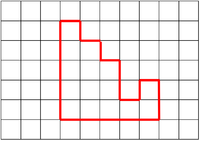
| − | | style="height:20px; width:200px; text-align:center;" |This shape has an area of 15 [[square]]s. | + | | style="height:20px; width:200px; text-align:center;" |This shape has an [[area]] of 15 [[square]]s. |
|} | |} | ||
| Line 30: | Line 30: | ||
| style="height:20px; width:200px; text-align:center;" |The shape has 20 [[square]]s inside it, so the [[area]] is 20 [[square]]s. | | style="height:20px; width:200px; text-align:center;" |The shape has 20 [[square]]s inside it, so the [[area]] is 20 [[square]]s. | ||
| style="height:20px; width:200px; text-align:center;" |This shape has an [[area]] of 14 [[square]]s. | | style="height:20px; width:200px; text-align:center;" |This shape has an [[area]] of 14 [[square]]s. | ||
| − | | style="height:20px; width:200px; text-align:center;" |This shape has an area of 15 [[square]]s. | + | | style="height:20px; width:200px; text-align:center;" |This shape has an [[area]] of 15 [[square]]s. |
|} | |} | ||
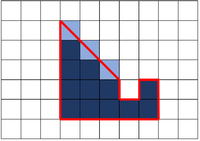
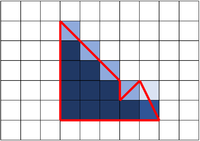
: If an unusual shape is drawn on a grid the [[area]] can be [[estimate]]d. The answer will not be exactly correct, but it will be close. | : If an unusual shape is drawn on a grid the [[area]] can be [[estimate]]d. The answer will not be exactly correct, but it will be close. | ||
| Line 41: | Line 41: | ||
| style="height:20px; width:200px; text-align:center;" |This shape has 12 full [[square]]s and 3 half [[square]]s. So the [[area]] is 12 + 3.5 = 15.5 squares. | | style="height:20px; width:200px; text-align:center;" |This shape has 12 full [[square]]s and 3 half [[square]]s. So the [[area]] is 12 + 3.5 = 15.5 squares. | ||
| style="height:20px; width:200px; text-align:center;" |This shape has 10 full [[square]]s, 2/3 of a [[square]], 4 half [[square]]s and 1/3 of a [[square]]. So the [[area]] is 10 + 2/3 + 4 + 1/3 = 15 [[square]]s. | | style="height:20px; width:200px; text-align:center;" |This shape has 10 full [[square]]s, 2/3 of a [[square]], 4 half [[square]]s and 1/3 of a [[square]]. So the [[area]] is 10 + 2/3 + 4 + 1/3 = 15 [[square]]s. | ||
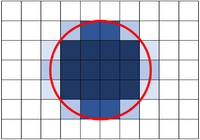
| − | | style="height:20px; width:200px; text-align:center;" |This | + | | style="height:20px; width:200px; text-align:center;" |This circle has 12 full [[square]]s, 4 nearly full [[square]]s, 4 nearly empty [[square]]s, 6 half squares. The [[area]] is difficult to [[estimate]] but it is around 19 [[square]]s. |
|} | |} | ||
| + | : The [[unit]]s of [[area]] are not usually '[[square]]s', they are either [[Metres Squared|metres squared]] (m<sup>2</sup>) or [[Centimetres Squared|centimetres squared]] (cm<sup>2</sup>). | ||
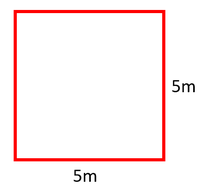
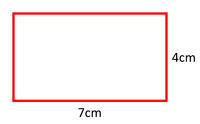
: The [[area]] of a [[rectangle]] or a [[square]] can also be found if the length of the sides is known. | : The [[area]] of a [[rectangle]] or a [[square]] can also be found if the length of the sides is known. | ||
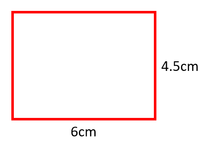
| − | : To find the [[area]] of a [[rectangle]] or [[square]] | + | : To find the [[area]] of a [[rectangle]] or [[square]]; multiply the [[base]] by the [[height]]. |
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | |[[File:SqaureArea1.png|center|200px]] | ||
| + | |[[File:RectangleArea1.png|center|200px]] | ||
| + | |[[File:RectangleArea2.png|center|200px]] | ||
| + | |- | ||
| + | | style="height:20px; width:200px; text-align:center;" | | ||
| + | <math>area = base \times height</math> | ||
| + | |||
| + | <math>area = 5 \times 5</math> | ||
| + | |||
| + | <math>area = 25m^2</math> | ||
| + | |||
| + | | style="height:20px; width:200px; text-align:center;" | | ||
| + | <math>area = base \times height</math> | ||
| + | |||
| + | <math>area = 7 \times 4</math> | ||
| + | |||
| + | <math>area = 28cm^2</math> | ||
| + | |||
| + | | style="height:20px; width:200px; text-align:center;" | | ||
| + | <math>area = base \times height</math> | ||
| + | |||
| + | <math>area = 6\times 4.5</math> | ||
| + | |||
| + | <math>area = 27cm^2</math> | ||
| + | |||
| + | |} | ||
| + | |||
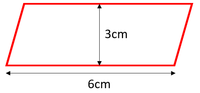
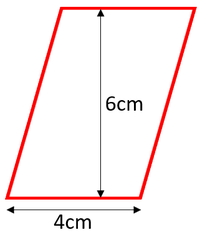
| + | : The [[area]] of parallelograms can be found by multiplying the [[base]] by the [[height]]. | ||
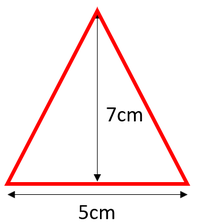
| + | : The [[area]] of a triangle can be found by multiplying half the [[base]] by the [[height]]. | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | |[[File:ParallelogramArea1.png|center|200px]] | ||
| + | |[[File:ParallelogramArea2.png|center|200px]] | ||
| + | |[[File:TriangleArea1.png|center|200px]] | ||
| + | |- | ||
| + | | style="height:20px; width:200px; text-align:center;" | | ||
| + | <math>area = base \times height</math> | ||
| + | |||
| + | <math>area = 6 \times 3</math> | ||
| + | |||
| + | <math>area = 18cm^2</math> | ||
| + | | style="height:20px; width:200px; text-align:center;" | | ||
| + | <math>area = base \times height</math> | ||
| + | |||
| + | <math>area = 4 \times 6</math> | ||
| + | |||
| + | <math>area = 24cm^2</math> | ||
| + | | style="height:20px; width:200px; text-align:center;" | | ||
| + | <math>area = \frac{1}{2} \times base \times height</math> | ||
| + | |||
| + | <math>area = \frac{1}{2} \times 5 \times 7</math> | ||
| + | |||
| + | <math>area = 17.5cm^2</math> | ||
| + | |} | ||
| + | |||
| + | ==Key Stage 3== | ||
| + | ===Meaning=== | ||
| + | [[Area]] is the size of a surface. | ||
| + | |||
| + | ===About Area=== | ||
| + | : The [[unit]]s of [[area]] are [[Metres Squared|metres squared]] or [[Centimetres Squared|centimetres squared]]. | ||
| + | |||
| + | ===Equations=== | ||
| + | ====Area of a Rectangle==== | ||
| + | <math>area = base \times height</math> | ||
| + | |||
| + | <math>a = b\times h</math> | ||
| + | |||
| + | ====Area of a Triangle==== | ||
| + | <math>area = \frac{1}{2} \times base \times height</math> | ||
| + | |||
| + | <math>a = \frac{b \times h}{2}</math> | ||
| + | |||
| + | ====Area of a Trapezium==== | ||
| + | <math>area = \frac{1}{2} \times (shortside+longside) \times height</math> | ||
| + | |||
| + | <math>a = \frac{1}{2} \times (A+B) \times height</math> | ||
| + | |||
| + | ====Area of a Circle==== | ||
| + | <math>area = \pi \times (radius)^2</math> | ||
| + | |||
| + | <math>a = \pi r^2</math> | ||
| + | |||
| + | ==Key Stage 4== | ||
| + | ===Meaning=== | ||
| + | [[Area]] is the size of a surface. | ||
| + | |||
| + | ===About Area=== | ||
| + | : The [[unit]]s of [[area]] are [[Metres Squared|metres squared]] or [[Centimetres Squared|centimetres squared]]. | ||
| + | |||
| + | ===Equations=== | ||
| + | ====Area of a Rectangle==== | ||
| + | <math>area = base \times height</math> | ||
| + | |||
| + | <math>a = b\times h</math> | ||
| + | |||
| + | ====Area of a Triangle==== | ||
| + | <math>area = \frac{1}{2} \times base \times height</math> | ||
| + | |||
| + | <math>a = \frac{b \times h}{2}</math> | ||
| + | |||
| + | ====Area of a Trapezium==== | ||
| + | <math>area = \frac{1}{2} \times (shortside+longside) \times height</math> | ||
| + | |||
| + | <math>a = \frac{1}{2} \times (A+B) \times height</math> | ||
| + | |||
| + | ====Area of a Circle==== | ||
| + | <math>area = \pi \times (radius)^2</math> | ||
| + | |||
| + | <math>a = \pi r^2</math> | ||
| + | |||
| + | ====Surface Area of a Sphere==== | ||
| + | <math>area = 4 \times \pi \times (radius)^2</math> | ||
| + | |||
| + | <math>a = 4 \pi r^2</math> | ||
| + | |||
| + | ====Surface Area of a Cylinder==== | ||
| + | <math>area = 2 \times \pi \times (radius)^2 + 2 \times \pi \times radius \times height</math> | ||
| + | |||
| + | <math>a = 2 \pi r^2 + 2 \pi rh</math> | ||
Latest revision as of 17:23, 8 April 2019
Lower Key Stage 2
Meaning
Area is the size of a surface.
About Area
- If a rectilinear shape is drawn on a grid the area can be found by counting the number of squares inside the shape.
| The shape has 20 squares inside it, so the area is 20 squares. | This shape has an area of 14 squares. | This shape has an area of 15 squares. |
Upper Key Stage 2
Meaning
Area is the size of a surface.
About Area
- If a rectilinear shape is drawn on a grid the area can be found by counting the number of squares inside the shape.
| The shape has 20 squares inside it, so the area is 20 squares. | This shape has an area of 14 squares. | This shape has an area of 15 squares. |
- If an unusual shape is drawn on a grid the area can be estimated. The answer will not be exactly correct, but it will be close.
| This shape has 12 full squares and 3 half squares. So the area is 12 + 3.5 = 15.5 squares. | This shape has 10 full squares, 2/3 of a square, 4 half squares and 1/3 of a square. So the area is 10 + 2/3 + 4 + 1/3 = 15 squares. | This circle has 12 full squares, 4 nearly full squares, 4 nearly empty squares, 6 half squares. The area is difficult to estimate but it is around 19 squares. |
- The units of area are not usually 'squares', they are either metres squared (m2) or centimetres squared (cm2).
- The area of a rectangle or a square can also be found if the length of the sides is known.
- To find the area of a rectangle or square; multiply the base by the height.
|
\(area = base \times height\) \(area = 5 \times 5\) \(area = 25m^2\) |
\(area = base \times height\) \(area = 7 \times 4\) \(area = 28cm^2\) |
\(area = base \times height\) \(area = 6\times 4.5\) \(area = 27cm^2\) |
- The area of parallelograms can be found by multiplying the base by the height.
- The area of a triangle can be found by multiplying half the base by the height.
|
\(area = base \times height\) \(area = 6 \times 3\) \(area = 18cm^2\) |
\(area = base \times height\) \(area = 4 \times 6\) \(area = 24cm^2\) |
\(area = \frac{1}{2} \times base \times height\) \(area = \frac{1}{2} \times 5 \times 7\) \(area = 17.5cm^2\) |
Key Stage 3
Meaning
Area is the size of a surface.
About Area
- The units of area are metres squared or centimetres squared.
Equations
Area of a Rectangle
\(area = base \times height\)
\(a = b\times h\)
Area of a Triangle
\(area = \frac{1}{2} \times base \times height\)
\(a = \frac{b \times h}{2}\)
Area of a Trapezium
\(area = \frac{1}{2} \times (shortside+longside) \times height\)
\(a = \frac{1}{2} \times (A+B) \times height\)
Area of a Circle
\(area = \pi \times (radius)^2\)
\(a = \pi r^2\)
Key Stage 4
Meaning
Area is the size of a surface.
About Area
- The units of area are metres squared or centimetres squared.
Equations
Area of a Rectangle
\(area = base \times height\)
\(a = b\times h\)
Area of a Triangle
\(area = \frac{1}{2} \times base \times height\)
\(a = \frac{b \times h}{2}\)
Area of a Trapezium
\(area = \frac{1}{2} \times (shortside+longside) \times height\)
\(a = \frac{1}{2} \times (A+B) \times height\)
Area of a Circle
\(area = \pi \times (radius)^2\)
\(a = \pi r^2\)
Surface Area of a Sphere
\(area = 4 \times \pi \times (radius)^2\)
\(a = 4 \pi r^2\)
Surface Area of a Cylinder
\(area = 2 \times \pi \times (radius)^2 + 2 \times \pi \times radius \times height\)
\(a = 2 \pi r^2 + 2 \pi rh\)