Difference between revisions of "Wavelength"
(→Meaning) |
|||
| Line 15: | Line 15: | ||
==Key Stage 4== | ==Key Stage 4== | ||
===Meaning=== | ===Meaning=== | ||
| − | [[Wavelength]] is the distance between two identical points on adjacent [[ | + | [[Wavelength]] is the distance between two identical points on adjacent [[wave]]s. |
===About Wavelength=== | ===About Wavelength=== | ||
Revision as of 14:19, 3 April 2019
Contents
Key Stage 3
Meaning
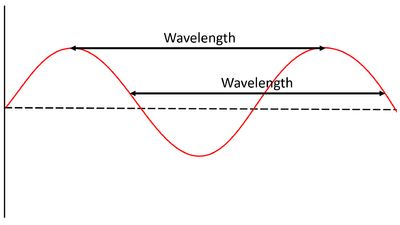
Wavelength is the distance between a point on one wave and an identical point on the next wave.
About Wavelength
- Wavelength is measured in metres.
| The wavelength is the length of one wave including the peak and trough. |
Key Stage 4
Meaning
Wavelength is the distance between two identical points on adjacent waves.
About Wavelength
- Wavelength is a scalar quantity because it has magnitude only.
- The SI Unit of wavelength is the metre.
| The wavelength is the length of one wave including the peak and trough. |
Equation
NB: You should remember this equation with v as the subject of the formula. Wavelength = (Wave Speed)/(Frequency)
\( \lambda = \frac{v}{f}\)
Where\[ \lambda\] = The wavelength of the wave.
\(v\) = The wave speed of the wave.
\(f\) = The frequency of the wave.
Example Calculations
| A wave with frequency 700Hz travels at a speed of 340m/s. Calculate the wavelength of the wave correct to two significant figures. | A 630MHz radiowave travels at 300,000,000m/s in a vacuum. Calculate the wavelength of this radiowave correct to two significant figures. |
| 1. State the known quantities
f = 700Hz v = 340m/s |
1. State the known quantities
f = 630MHz = 630x106Hz v = 300,000,000m/s = 3x108m/s |
| 2. Substitute the numbers into the equation and solve.
\( \lambda = \frac{v}{f}\) \( \lambda = \frac{340}{700}\) \( \lambda = 0.48571m\) \( \lambda \approx 0.48m\) |
2. Substitute the numbers into the equation and solve.
\( \lambda = \frac{v}{f}\) \( \lambda = \frac{630 \times 10^6}{3 \times 10^8}\) \( \lambda = 2.1m\) |